Algoritma Dijkstra

Algoritma Dijkstra, dinamakan sesuai dengan nama penemunya, seorang ilmuwan komputer berkebangsaan Belanda yang bernama Edsger Dijkstra, adalah algoritma yang digunakan untuk mencari lintasan terpendek pada sebuah graf berarah.

Cara kerja algoritma Dijkstra memakai stategi greedy, dimana pada setiap langkah dipilih sisi dengan bobot terkecil yang menghubungkan sebuah simpul yang sudah terpilih dengan simpul lain yang belum terpilih.

Algoritma ini mirip dengan algoritma Prim untuk mencari MST, yaitu pada tiap iterasi memeriksa sisi-sisi yang menghubungkan subset verteks W dan subset verteks (V-W) dan memindahkan verteks w dari (V-W) ke W yang memenuhi kriteria tertentu. Perbedaannya terletak pada kriteria itu sendiri.

• Jika yang dicari algoritma Kruskal adalah sisi dengan bobot terkecil dari sisi-sisi di atas dalam setiap iterasinya,

• dalam algoritma Dijkstra, yang dicari adalah sisi yang menghubungkan ke suatu verteks di (V-W) sehingga jarak dari verteks asal Vs ke verteks tersebut adalah minimal.

Contoh Soal :

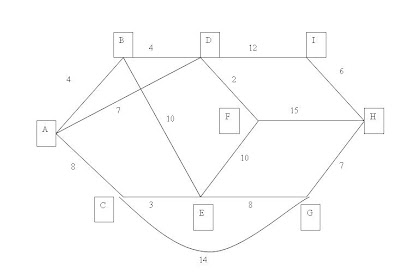
Mencari jalur teroptimal dari node A menuju node H

Iterasi I

Di mulai dari node A

d(B) = 4

d(C) = 8

d(D) = 7

d(E) = ∞

d(F) = ∞

d(G) = ∞

d(H) = ∞

d(I) = ∞

Dari node A menuju node B berbobot 4, menuju node C berbobot 8, menuju node D bebrobot 7. Sedangkan rute dari node A menuju node E, F,G, H dan I berbobot tidak hingga karena dari node A tidak ada jalur untuk menuju node-node tersebut. Dari hasil bobot node diatas di ambil jalur ke node B karena bobotnya paling kecil dari semuanya. Jadi rute yang terbentuk adalah dari node A menuju node B, karena bobot rute tersebut paling kecil dari semuanya.

Iterasi II

Di mulai dari node B

d(C) = min(d(C), d(B)+d(C))= min(8, 4+∞)= 8

d(D) = min(d(D), d(B)+d(D))= min(7, 4+8)= 7

d(E) = min(d(E), d(B)+d(E))= min(∞, 4+10)= 14

d(F) = min(d(F), d(B)+d(F))= min(∞, 4+∞)= ∞

d(G) = min(d(G), d(B)+d(G))= min(∞, 4+∞)= ∞

d(H) = min(d(H), d(B)+d(H))= min(∞, 4+∞)= ∞

d(I) = min(d(I), d(B)+d(I))= min(∞, 4+∞)= ∞

Mengapa tak ada jalur dari node B menuju node A? Karena node A sudah terlewati atau dengan kata lain sudah terbentuk jalur dari node A ke node B, maka tidak perlu di catat lagi. Dari hasil bobot node diatas di ambil jalur ke node D karena bobotnya paling kecil dari semuanya. Penjelasan rumus untuk mencari jarak minimum antar node sebagai berikut bobot jarak node yang dituju = minimum dari bobot jarak node sebelumnya dibandingkan dengan jumlah bobot dari node awal sekarang dengan jarak ke node yang akan dituju. Jadi rute yang terbentuk adalah dari node A menuju node D, karena bobot rute tersebut paling kecil dari semuanya. Mengapa rutenya berubah menjadi node A ke node D? Bukan ke node B ke node D? Karena pada perhitungan rumus di node D nilai bobot yang dihasilkan berasal dari perhitungan di iterasi I atau node A. d(D) = min(d(D), d(B)+d(D))= min(7, 4+8)= 7 (nilai 7 di ambil dari perhitungan di node sebelumnya yaitu node A atau iterasi I).

Iterasi III

Di mulai dari node D

d(C) = min(d(C), d(D)+d(C))= min(8, 7+∞)= 8

d(E) = min(d(E), d(D)+d(E))= min(14, 7+∞)= 14

d(F) = min(d(F), d(D)+d(F))= min(∞, 7+2)= 9

d(G) = min(d(G), d(D)+d(G))= min(∞, 7+∞)= ∞

d(H) = min(d(H), d(D)+d(H))= min(∞, 7+∞)= ∞

d(I) = min(d(I), d(D)+d(I))= min(∞, 7+12)= 19

Dari hasil bobot node diatas di ambil jalur ke node C karena bobotnya paling kecil dari semuanya. Jadi rute yang terbentuk adalah dari node A menuju node C, karena bobot rute tersebut paling kecil dari semuanya. Sama halnya pada iterasi II nilai dari node C diambil dari node sebelumnya yaitu perhitungan di node A atau iterasi I.

Iterasi IV

Di mulai dari node C

d(E) = min(d(E), d(C)+d(E))= min(14, 8+3)= 11

d(F) = min(d(F), d(C)+d(F))= min(9, 8+∞)= 9

d(G) = min(d(G), d(C)+d(G))= min(∞, 8+14)= 22

d(H) = min(d(H), d(C)+d(H))= min(∞, 8+∞)= ∞

d(I) = min(d(I), d(C)+d(I))= min(19, 8+∞)= 19

Dari hasil bobot node diatas di ambil jalur ke node F karena bobotnya paling kecil dari semuanya. Jadi rute yang terbentuk adalah dari node D menuju node F, karena bobot rute tersebut paling kecil dari semuanya dan bobot atau nilai rute ke node F di ambil dari perhitungan di node D atau iterasi III sehingga rute yang terbentuk dari node D ke node F.

Iterasi V

Di mulai dari node F

d(E) = min(d(E), d(F)+d(E))= min(11, 9+8)= 11

d(G) = min(d(G), d(F)+d(G))= min(22, 9+∞)= 22

d(H) = min(d(H), d(F)+d(H))= min(∞, 9+15)= 24

d(I) = min(d(I), d(F)+d(I))= min(19, 9+∞)= 19

Dari hasil bobot node diatas di ambil jalur ke node E karena bobotnya paling kecil dari semuanya. Jadi rute yang terbentuk adalah dari node C menuju node E, karena bobot rute tersebut paling kecil dari semuanya dan bobot atau nilai rute ke node E di ambil dari perhitungan di node C atau iterasi IV sehingga rute yang terbentuk dari node C ke node E.

Iterasi VI

Di mulai dari node E

d(G) = min(d(G), d(E)+d(G))= min(22, 11+8)= 19

d(H) = min(d(H), d(E)+d(H))= min(∞,11+15)= 24

d(I) = min(d(I), d(E)+d(I))= min(19, 11+∞)= 19

Dari hasil bobot node diatas di ambil jalur ke node E karena bobotnya paling kecil dari semuanya. Jadi rute yang terbentuk adalah dari node E menuju node G, karena bobot rute tersebut paling kecil dari semuanya dan bobot atau nilai rute ke node G di ambil dari perhitungan di node E atau iterasi VI sehingga rute yang terbentuk dari node E ke node G.

Iterasi VII

Di mulai dari node G

d(H) = min(d(H), d(G)+d(H))= min(24,19+7)= 24

d(I) = min(d(I), d(G)+d(I))= min(19, 19+∞)= 19

Dari hasil bobot node diatas di ambil jalur ke node I karena bobotnya paling kecil dari semuanya. Jadi rute yang terbentuk adalah dari node D menuju node I, karena bobot rute tersebut paling kecil dari semuanya dan bobot atau nilai rute ke node I di ambil dari perhitungan di node D atau iterasi III sehingga rute yang terbentuk dari node D ke node I.

Iterasi VIII

Di mulai dari node I

d(H) = min(d(H), d(I)+d(H))= min(24,19+6)= 24

Jadi rute yang terbentuk adalah dari node F menuju node H, karena bobot rute tersebut paling kecil dari semuanya dan bobot atau nilai rute ke node H di ambil dari perhitungan di node F atau iterasi V sehingga rute yang terbentuk dari node F ke node H.

Karena sudah mencapai node yang dituju yaitu node H maka mulailah proses pencarian jarak yang optimal dengan mengkalkulasi jarak-jarak yang sudah ditemukan.

Jadi rute yang optimal dari node A ke node H adalah melewati node A menuju node D, node D menuju node F, node F menuju node H dengan nilai total atau bobot total adalah 24.